The spread of new technologies leads to a crucial role for the modeling of 3D objects, and in particular for shape modeling, in many applications.
Actually, most of the information our senses collect is visual and shape-oriented, and most of our knowledge about the physical world comes as a shape information: reasoning about shape is a common way of describing real objects in engineering, architecture, medicine, biology, physics, and in daily life.
Geometric modeling has been a key research topic at IMATI - Dept. of Genova for several years, based on mathematical and computer science techniques related to geometry, computational topology and computer graphics. The main aim is to describe the shape and other geometric features of an object through geometric basic entities (points, lines, surfaces, volumes) used to build more complex shapes. More precisely, relations between mathematical model, computational model and graphical representation of objects in simulation and visualization systems are studied.
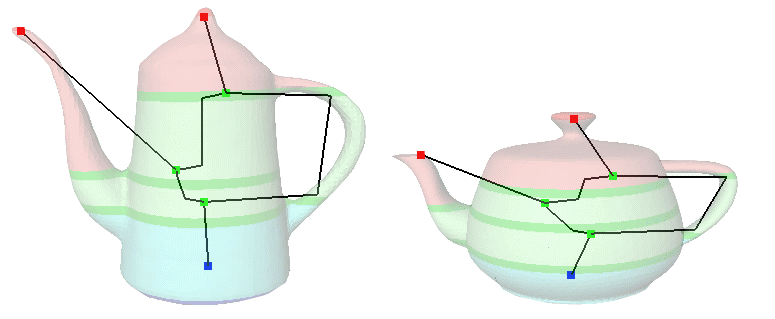
We aim at the definition of new models and methods for representation, analysis and handling of geometric information. The need for more structured models with higher descriptive capabilities grows with the morphological complexity of the represented objects. Thus, a good model should minimize the quantity of data necessary to build the mathematical representation, while maximizing the reliability of the result. A key point is to overcome the traditional approach by introducing representations able to operate at the semantic level we normally use to code our perception of a shape.
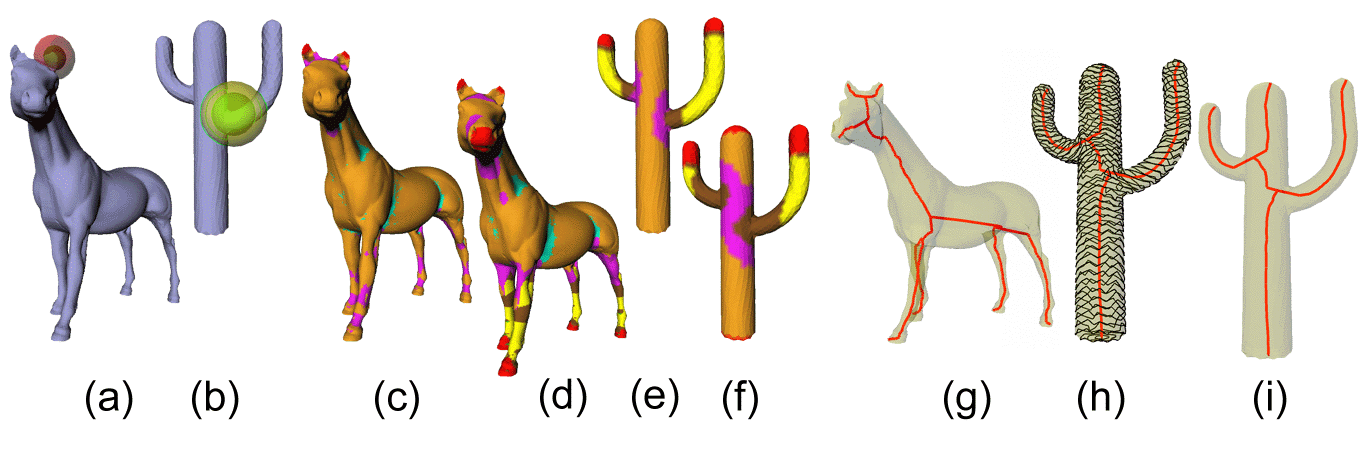
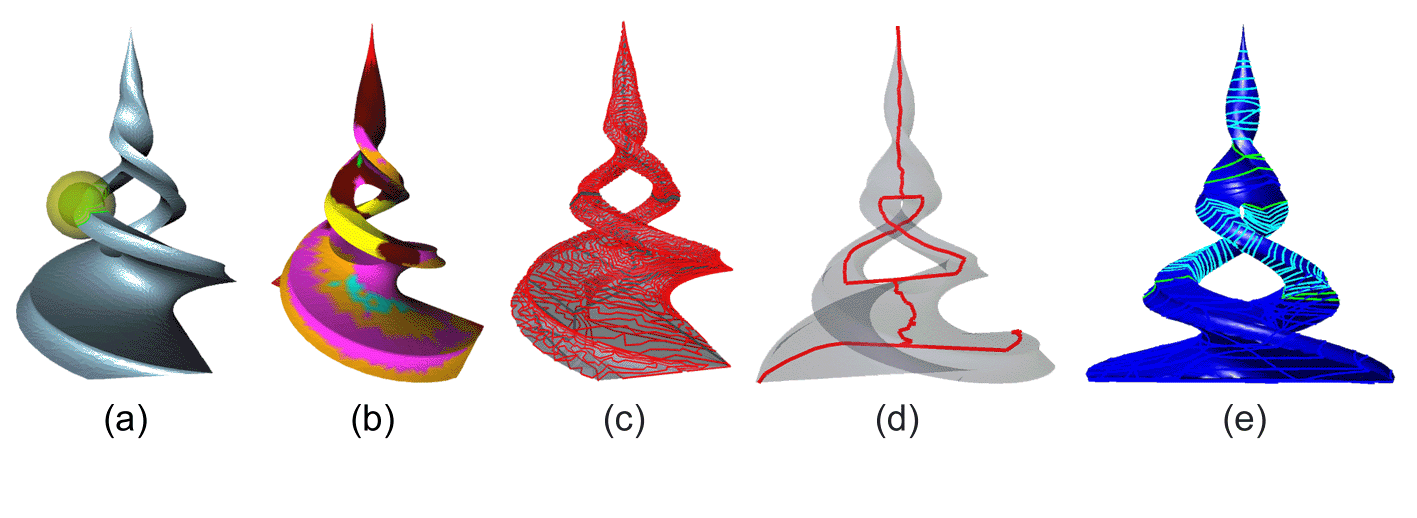
It is then necessary to identify properties or features which can be used to describe objects in an effective and concise way, and to give them a formal definition so that they can be easily associated to a geometric representation. To this aim, techniques for simplification of the geometric model have shown very useful, because they can eliminate non-significant details from the representation, thus reducing the number of geometric entities. This operation preserves the main shape features, such as curvature properties or characteristic lines, and may be considered as an abstraction tool which allows the user to describe the object at different levels of detail.
Besides these geometric simplification techniques, widely used in computer graphics, also computational topology offers interesting hints to shape description. Actually, extraction of topological structures, e.g. critical point configurations or contour line evolution along prevalent directions, constitutes a powerful technique for shape abstraction.
The main application fields are spatial data handling (digital terrain modeling and geographical information systems) and industrial design. On these topics 8 Projects are currently carried on (3 international, 3 Joint Projects, 2 national) as well as a number of collaborations with Universities, Research centers and Industries.
Vedi anche:
Immagini: